C/ Quels noyaux utiliser sur Terre ?

Dans le but de réaliser une réaction de fusion, il est nécessaire d’amener deux noyaux très proches l’un de l’autre, de façon à ce que l’interaction forte agisse et fasse fusionner les noyaux ; cette fusion dégageant de l’énergie. Pour obtenir une réaction rentable énergétiquement, il est nécessaire de prendre en compte deux facteurs : l’énergie produite par la réaction, qui doit être importante, et l’énergie devant être apportée de façon à ce que la réaction se produise.
On considèrera pour la suite les notations du tableau ci-dessous, et on notera également El(X) l’énergie de liaison d’un noyau, Δm(X) son défaut de masse, et m(X) sa masse, et c la célérité de la lumière dans le vide : c = 2,997.10⁸ m. s^-1.

La répulsion entre différents noyaux :

Il convient tout d'abord de déterminer quels noyaux sont les plus intéressants à utiliser de façon à obtenir une réaction dégageant le plus d’énergie possible, tout en demandant un apport minimal d'énergie – pour être performante et justifier l’enjeu de l’utilisation de cette source d’énergie. On sait qu’un noyau atomique est constitué de protons et de neutrons. Les derniers sont électriquement neutres, et n’ont donc pas d’interaction électrostatique entre eux d’après la loi de Coulomb. Cependant, les protons possèdent tous une charge électrique positive de 1 e. Par conséquent, la charge électrique d’un noyau atomique est donnée par Z . e.
D’après la loi de Coulomb, puisque deux noyaux ont une charge électrique de même signe, ils se repoussent suivant une force dont la norme est donnée par

F = k x (| q x q’ |) / d², avec :

-  q et q’ = les charges électriques respectives des deux noyaux,

-   k = constante de la loi  coulomb

-  d = distance entre les 2 noyaux

  Le premier objectif est donc d’obtenir la force de répulsion la moins élevée en jouant sur les variables de cette formule. On a ici k, qui  ne peut pas varier car c’est une constante, d sera ici une constante également, dans la mesure où l’on souhaite rapprocher deux noyaux pour fusionner, donc à une distance égale au diamètre du noyau, soit de 2,0 x 10^-15 m. Par conséquent, seuls q et q’ peuvent varier, en sachant que q et q’ sont des multiples de la charge élémentaire qui, comme son nom l’indique, est indivisible (sauf pour les quarks). En sachant de plus qu’un noyau contient au moins un proton, q et q’ auront chacun pour valeur minimale e. Cela est possible en utilisant des noyaux d’hydrogène ou ses isotopes. Étant donné que la charge électrique augmente rapidement avec le nombre de nucléons puisque q = Z x e, on aura tout intérêt à prendre l’hydrogène ou un noyau contenant un numéro atomique au voisinage de 1 pour obtenir une fusion sans dépenser trop d’énergie. La probabilité de passage de barrière imposée par cette répulsion peut être quantifiée par la "section efficace". La variation, en fonction de l'énergie d'interaction utilisée, exprimée en keV, des sections efficaces de plusieurs réactions de fusion, est indiquée sur la courbe ci-dessous.

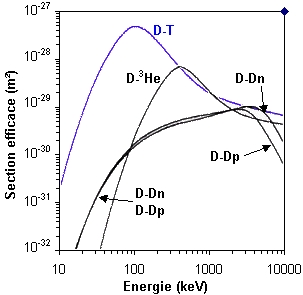
On remarque que c’est l’association du deutérium et de tritium qui couvre la plus grande section efficace tout en utilisant le moins d’énergie.

Energie libérée :

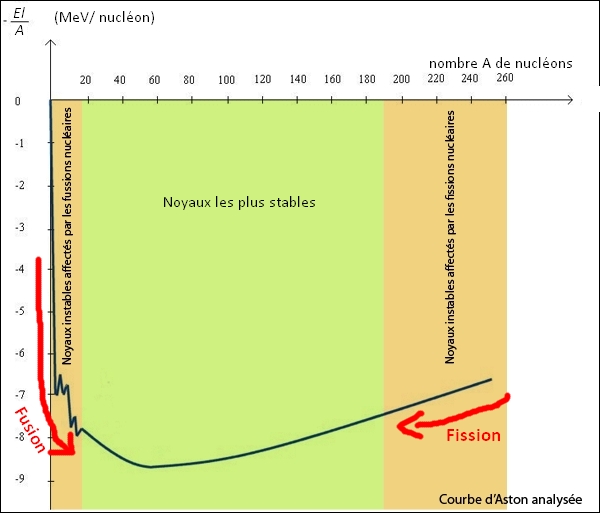
      Ilfaut maintenant calculer l’énergie libérée âpres une réaction de fusion pour savoir quelle réaction est la plus avantageuse en fonction de l’énergie produite : l’énergie dégagée correspond, comme vu précédemment, à ΔE = |m_produits – m_réactifs| . c². Ainsi, plus la somme des énergies de liaison des produits est grande par rapport à celle des énergies de liaison des réactifs, plus la réaction dégagera d’énergie. Afin de déterminer facilement les réactions les plus efficaces, on peut utiliser la courbe d’Aston, que nous avons vue précédemment : elle donne l’énergie de liaison par nucléon du noyau atomique : par conséquent, plus elle est basse, plus l’énergie de liaison par nucléon est importante, et donc plus une réaction présentera une grande différence vers le minimum de la courbe, plus elle libérera d’énergie.

On constate sur la courbe deux manières d’atteindre ce minimum : on peut réaliser des réactions de fusion de noyaux légers : alors les réactifs auront une énergie de liaison entre nucléons plus importante, mais on peut aussi réaliser des réactions de fission des noyaux lourds, dont le numéro atomique est élevé, de façon à obtenir des noyaux moins lourds (avec un nombre de nucléons A moins élevé) mais dont l’énergie de liaison par nucléon est plus importante.

Les réactions impliquant l’hydrogène ou ses isotopes ont l’air tout indiquées pour un choix de fusion, dans la mesure où, en plus d’être accessibles, on constate un décalage important entre les énergies de liaison des noyaux dont le nombre de masse est proche de 0, et de l’hélium 4, dont l’énergie de liaison par nucléon est d’environ 7 MeV. Ainsi, pour déterminer quelle réaction utiliser, il faut allons calculer et comparer les énergies produites par plusieurs réactions à ce niveau.

Voici les résultats fournis par le CEA :

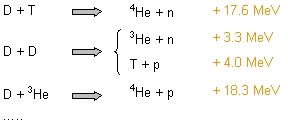
https://www-fusion-magnetique.cea.fr/fusion/principes/principes01.htm
 

Ainsi c’est la réaction D + ³He = ⁴He + p qui libère le plus d’énergie, or ce n’est pas la plus rentable car l’énergie à déployer pour faire fusionner est conséquente vu qu’il y a une plus grande répulsion entre les noyaux et le ³He est rare sur Terre. On utilisera donc la réaction

 D + T = ⁴He + n, qui libère le plus la deuxième plus grande quantité d’énergie tout en déployant le moins d’énergie possible pour faire fusionner les deux noyaux. IL faut donc maintenant reussir a appliquer cette réaction sur Terre.

Apres avoir étudier les principes et ce qu'est la fusion , nous allons maintenant nous pencher sur son utilisation sur Terre.